DeepSeek MoE

传送门：DeepSeekMoE: Towards Ultimate Expert Specialization in Mixture-of-Experts Language Models

本文提出了一种新的架构 DeepSeekMoE. 相比于 GShard MoE 架构，实现了更高的性能，同时降低了计算开销. 本文旨在提高专家的专业化程度，从而减少冗余. DeepSeekMoE 主要存在以下的创新：

(1) Fine-Grained Expert Segmentation. 在保持参数量不变的情况下，通过拆分 FFN 中间隐藏维度将专家细分为更细的粒度. 实际上就是在不变的参数量下，增加专家和 topK 的数量.

(2) Shared Expert Isolation. 将某些专家隔离，从而作为始终激活的共享专家，旨在捕捉和巩固不同上下文中的共同知识.

Structure

传统 Transformer 架构. 其中 \(T\) 为序列长度.

\[ \begin{aligned} \boldsymbol{u}_{1:T}^l &= \text{Self-Att}(\boldsymbol{h}_{1:T}^{l-1}) + \boldsymbol{h}_{1:T}^{l-1},\\ \boldsymbol{h}_{t}^l &= \text{FFN}(\boldsymbol{u}_t^l) + \boldsymbol{u}_t^l. \end{aligned}\]

传统 MoE 架构，在 Transformer 中以指定间隔用 MoE 层替代 FFN. 例如，我们将第 \(l\) 层 FFN 替换为 MoE.

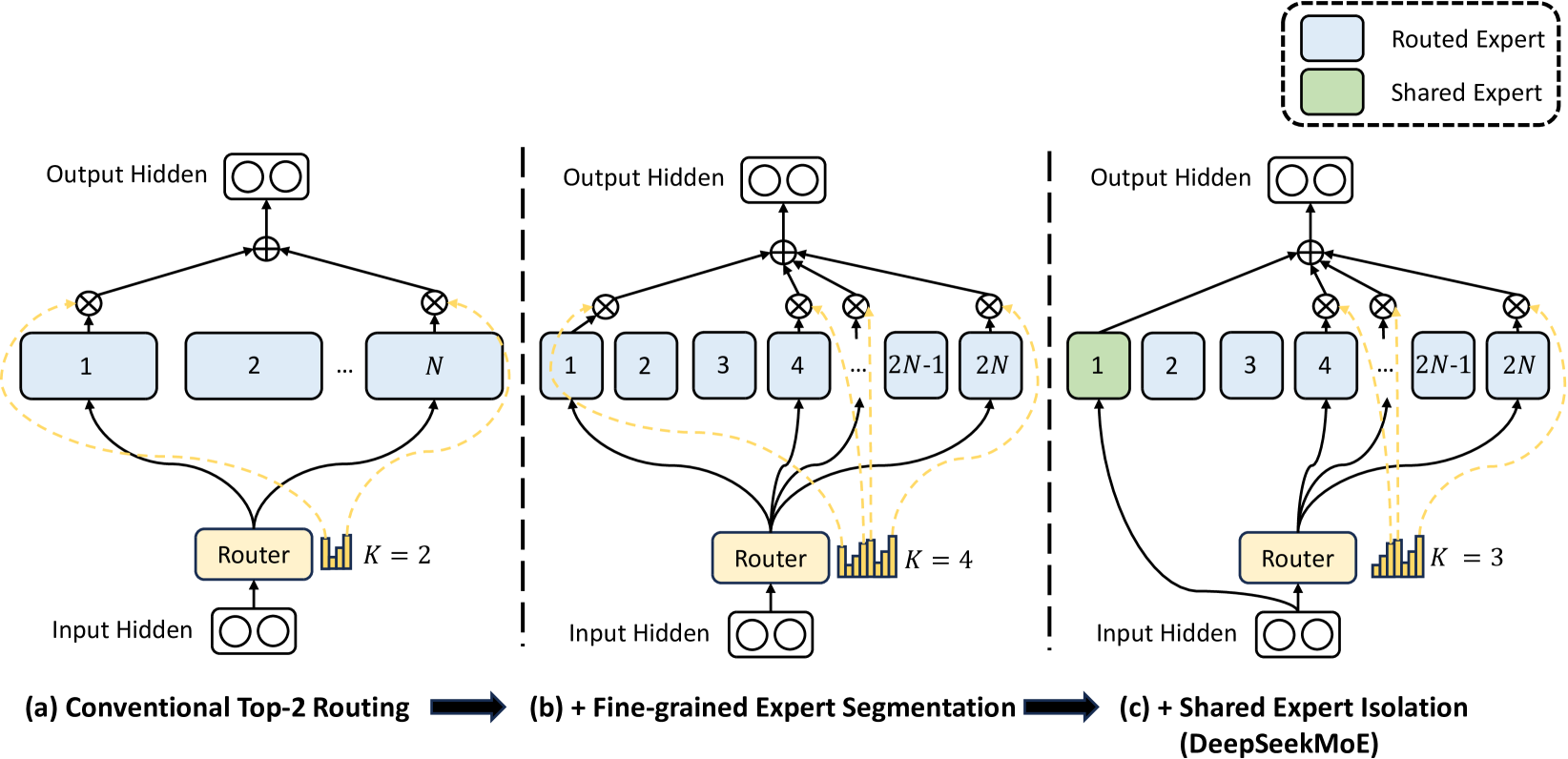
\[ \begin{aligned} \boldsymbol{h}_{t}^l &= \sum_{i=1}^N\left(g_{i, t}\text{FFN}_i(\boldsymbol{u}_t^l)\right) + \boldsymbol{u}_t^l,\\ g_{i, t} &= \begin{cases} s_{i, t}, &s_{i, t} \in \text{Topk}(\{s_{j, t} | j \in [N]\}, K)\\ 0, &\text{otherwise} \end{cases},\\ s_{i, t} &= \text{Softmax}(\boldsymbol{u}_t^{lT}\boldsymbol{e}_i^l). \end{aligned}\]

DeepSeek MoE 架构如下. 其中共享专家的数量是 \(K_S\) 个.

\[ \begin{aligned} \boldsymbol{h}_{t}^l &= \sum_{i=1}^{K_S} \text{FFN}_i(\boldsymbol{u}_t^l) + \sum_{i=K_S+1}^{mN}\left(g_{i, t}\text{FFN}_i(\boldsymbol{u}_t^l)\right) + \boldsymbol{u}_t^l,\\ g_{i, t} &= \begin{cases} s_{i, t}, &s_{i, t} \in \text{Topk}(\{s_{j, t} | K_S + 1 \le j \le mN\}, mK-K_S)\\ 0, &\text{otherwise} \end{cases},\\ s_{i, t} &= \text{Softmax}(\boldsymbol{u}_t^{lT}\boldsymbol{e}_i^l). \end{aligned}\]

为了加强负载的均衡性（不均衡的负载可能导致专家训练的不充分、加剧分布式推理瓶颈），DeepSeek MoE 引入了专家级平衡损失和设备级平衡损失. 设 \(N'=mN-K_S\) 为路由专家数，\(K'=mK-K_S\) 为选择的路由专家数.

Expert-Level Balance Loss. 用于降低路由崩溃的风险.

\[\mathscr{L}_{\text{ExpBal}}=\alpha_1\sum_{i=1}^{N'}f_iP_i=\alpha_1\left(\sum_{i=1}^{N'}\left(\dfrac{N'}{K'T}\sum_{t=1}^T \mathbb{1}(\text{Token }t\text{ selects Expert }i)\right)\times \left(\frac{1}{T}\sum_{t=1}^T s_{i, t}\right)\right).\]

考虑第一项 \(f_i\)，完全平均时，每个路由专家被选中 \(\frac{K'T}{N'}\) 次，通过缩放进行了归一化. 第二项 \(P_i\) 是第 \(i\) 个专家被选择的概率的期望.

Device-Level Balance Loss. 用于缓解计算瓶颈. 其中专家分布在 \(D\) 台设备上，每台设备上的专家数是 \(\mathscr{E}_i\).

\[\mathscr{L}_{\text{DevBal}} = \alpha_2\sum_{i=1}^D f_i' P_i'=\alpha_2\left(\sum_{i=1}^{N'}\left(\frac{1}{|\mathscr{E}_i|}\sum_{j\in \mathscr{E}_i}f_j\right)\times \left(\sum_{j\in \mathscr{E}_i} P_j\right)\right).\]

在实践中，取较小的 \(\alpha_1\) 来降低路由崩溃的风险，取较大的 \(\alpha_2\) 来缓解计算瓶颈.

Experiments

本文使用 MoE 层替换所有 FFN 层，并确保专家参数的总数是标准 FFN 的 16 倍. 其中，激活的专家参数数为标准 FFN 的 2 倍. 实验中，DeepSeekMoE 采用 1 + 63 的专家配置，这意味着与 Dense x16 相比，单个专家的相对大小是 0.25. 然后，DeepSeekMoE 激活了 1 + 7 个专家，因此与 Dense x16 相比，激活的参数量是 0.25 倍. 实验说明，DeepSeekMoE 与 Dense 模型的表现（也就是控制总参数量，MoE 的理论表现应当弱于 Dense 模型，这是 MoE 表现的理论上界）紧密对齐.

通过消融实验，本文证明了共享专家隔离、精细专家分割的重要性. 同时，通过观察 top routed experts 失效后的结果，本文证明了专家的专业化程度比 GShard 方法更高. 更进一步，通过禁用共享专家而将参数分配到路由专家上，模型的表现（Pile Loss）下降，证明了共享专家不能被路由专家替代.

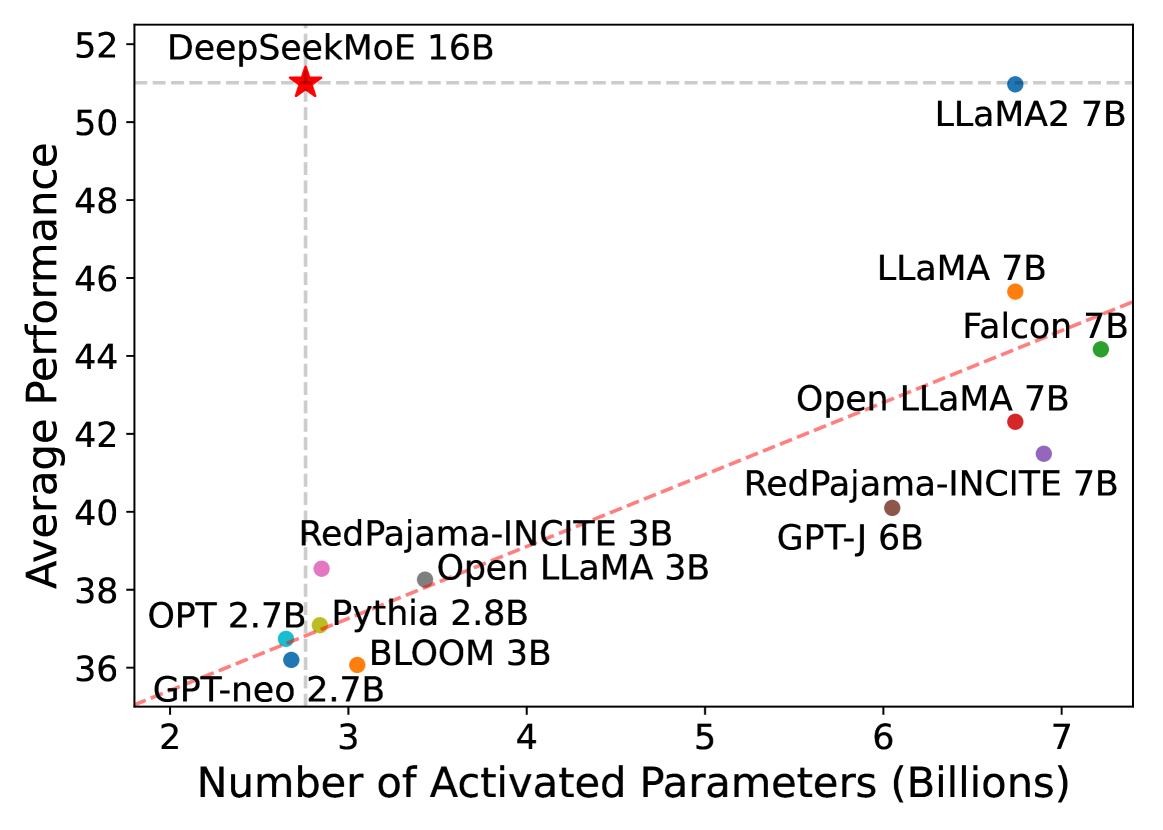
接着，本文将参数扩展到 DeepSeek MoE 16B，证明了与 LLaMA2 7B 相比，DeepSeekMoE 以约 40% 的计算量实现了更优的性能.

本页面最近更新：，更新历史
发现错误？想一起完善？在 GitHub 上编辑此页！
本页面贡献者：OI-wiki
本页面的全部内容在协议之条款下提供，附加条款亦可能应用