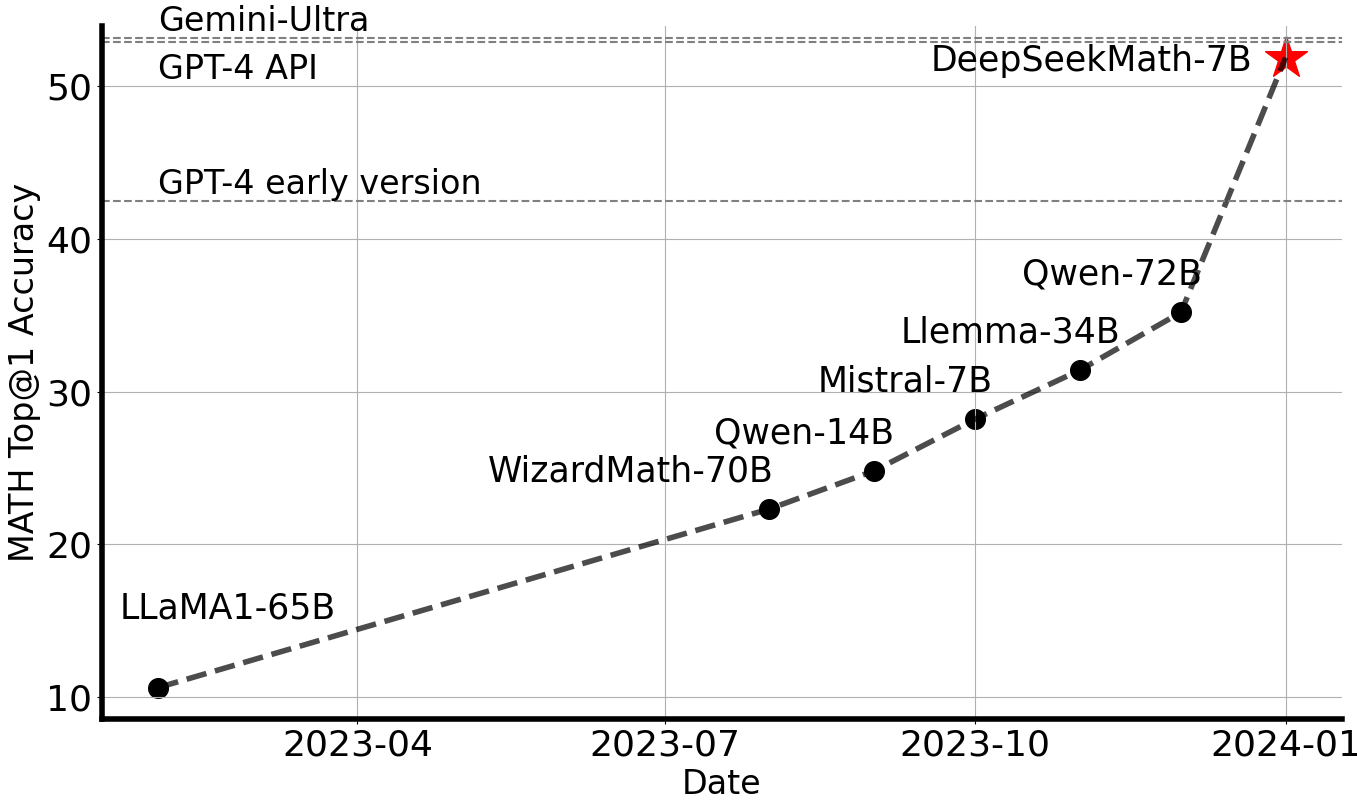
DeepSeek Math

传送门：DeepSeekMath: Pushing the Limits of Mathematical Reasoning in Open Language Models

笔者认为，本文最重要的贡献是提出了 GRPO 的强化学习算法. 通过舍弃 critic 模型，GRPO 显著减少了训练资源的使用. 当然本文还涉及数据集构建，预训练，监督微调等内容.

Structure

传统 PPO 架构. 这是一种经典的 actor-critic RL 算法.

\[\mathcal{J}_{PPO}(\theta) = \mathbb{E}_{q \sim P(Q), o \sim \pi_{\theta_{old}}(O|q)} \frac{1}{|o|} \sum_{t=1}^{|o|} \min \left[ \frac{\pi_\theta(o_{t} | q, o_{<t})}{\pi_{\theta_{old}}(o_{t} | q, o_{<t})} A_{t}, \text{clip} \left( \frac{\pi_\theta(o_{t} | q, o_{<t})}{\pi_{\theta_{old}}(o_{t} | q, o_{<t})}, 1 - \epsilon, 1 + \epsilon \right) A_{t} \right].\]

其中 \(\pi_\theta,\pi_{\theta_{old}}\) 是当前和旧的 policy model. \(q, o\) 是从问题数据集和旧策略 \(\pi_{\theta_{old}}\) 中抽样的问题和输出. \(\epsilon\) 是一个与裁剪有关的超参数，用于稳定训练，\(A_t\) 是优势，通过 GAE 计算，需要用到奖励 \(\{r_{\ge t}\}\) 和 value function \(V_{\psi}\). 为了防止 reward model 的过度优化，标准的方法是从参考模型上添加 KL penalty.

\[r_{t} = r_\phi(q, o_{\le t}) - \beta \log\frac{\pi_{\theta}(o_{t}|q, o_{<t})}{\pi_{ref}(o_{t}|q, o_{<t})}.\]

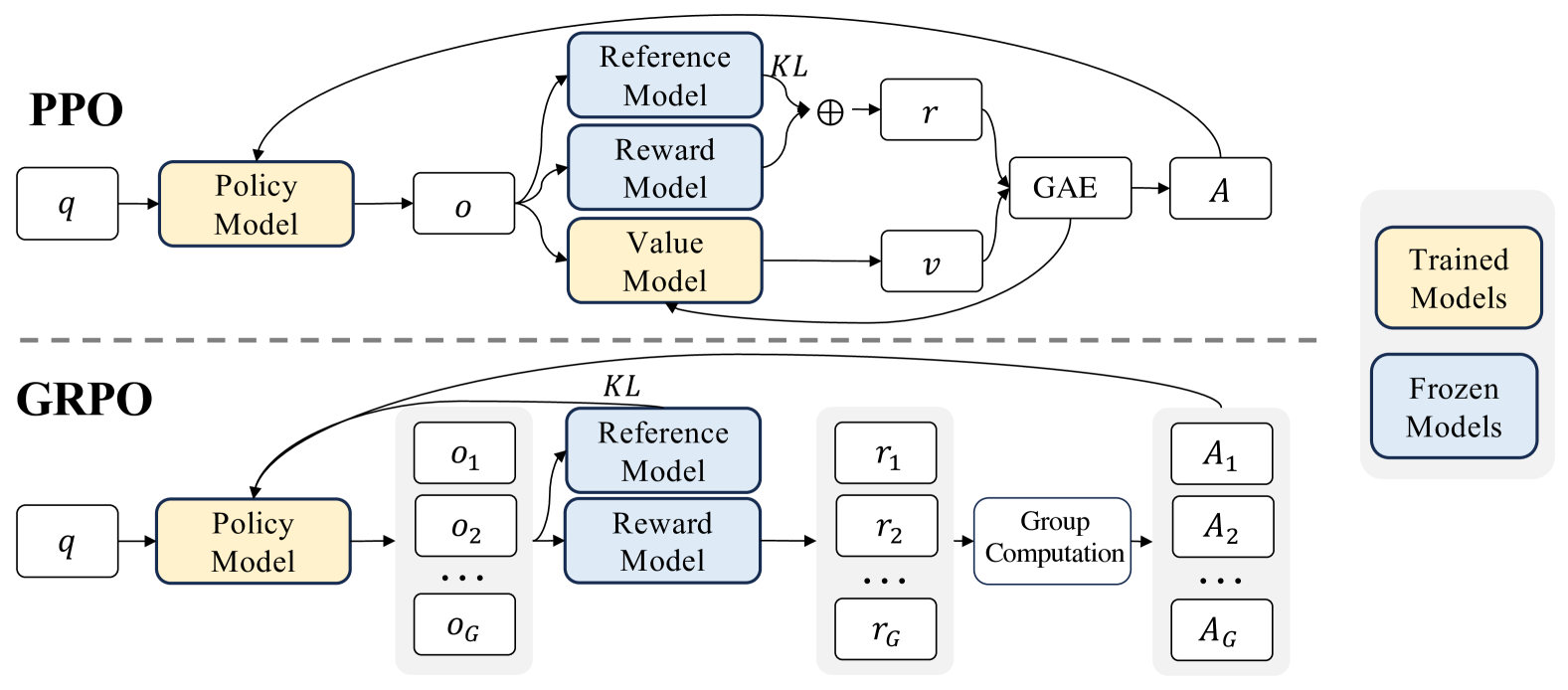
下面的 GRPO 算法省略了 value function. \(\hat{A}_{i,t}\) 是基于每组内部输出的相对奖励计算的优势.

\[ \begin{aligned} \mathcal{J}_{GRPO}(\theta) = &\mathbb{E}_{q \sim P(Q), \{o_i\}_{i=1}^G \sim \pi_{\theta_{old}}(O|q)} \frac{1}{G}\sum_{i=1}^G\frac{1}{|o_i|} \sum_{t=1}^{|o_i|} \\ &\left\{ \min \left[ \frac{\pi_\theta(o_{i,t} | q, o_{i,<t})}{\pi_{\theta_{old}}(o_{i,t} | q, o_{i,<t})} \hat{A}_{i,t}, \text{clip} \left( \frac{\pi_\theta(o_{i,t} | q, o_{i,<t})}{\pi_{\theta_{old}}(o_{i,t} | q, o_{i,<t})}, 1 - \epsilon, 1 + \epsilon \right) \hat{A}_{i,t} \right] - \beta \mathbb{D}_{KL}\left[\pi_{\theta} || \pi_{ref}\right]\right\}. \end{aligned} \]

与在线 RFT 相比，GRPO 通过根据奖励模型提供的奖励值独特地调整其梯度系数，从而可以根据响应的不同大小进行差异化强化与惩罚. 同时，通过直接将训练 policy 和参考 policy 的 KL penalty 添加到 loss 中，避免了之前 KL penalty 计算的复杂性. KL 散度通过下面的无偏估计量来估计.

\[\mathbb{D}_{KL}\left[\pi_{\theta} || \pi_{ref}\right] = \frac{\pi_{ref}(o_{i,t}|q,o_{i,<t})}{\pi_{\theta}(o_{i,t}|q,o_{i,<t})}- \log\frac{\pi_{ref}(o_{i,t}|q,o_{i,<t})}{\pi_{\theta}(o_{i,t}|q,o_{i,<t})} - 1>0.\]

Outcome Supervision RL. 对于每个问题 \(q\)，从旧的策略模型 \(\pi_{\theta_{old}}\) 中抽取一组输出 \(\{o_1,\cdots, o_G\}\). 然后，使用奖励模型对输出进行打分，相应地产生 \(G\) 个奖励 \(\textbf{r}=\{r_1,\cdots, r_G\}\). 接着定义 \(\hat{A}_{i, t}\) 为减去组均值后的归一化奖励

\[\hat{A}_{i, t} = \widetilde{r}_i = \frac{r_i- {\rm mean}(\mathbf{r})}{{\rm std}(\mathbf{r})}.\]

Process Supervision RL. 设 \(\text{index}(j)\) 为第 \(j\) 步，则奖励 \(\mathbf{R}=\{\{r_1^{\text{index}(1)}, \cdots,r_1^{\text{index}(K_1)}\},\cdots,\{r_G^{\text{index}(1)}, \cdots,r_G^{\text{index}(K_G)}\} \}\). 取

\[\hat{A}_{i, t} = \sum_{\text{index}(j) \ge t} \widetilde{r}_i^{\text{index}(j)}=\sum_{\text{index}(j) \ge t}\frac{r_i^{index(j)} - {\rm mean(\mathbf{R})}}{{\rm std(\mathbf{R})}}.\]

Iterative RL. 下面的算法展示了 GRPO 与迭代式 RL 的合成.

\[ \boxed{ \begin{array}{c} \textbf{Iterative Group Relative Policy Optimization} \\ \begin{array}{rl} \textbf{Inp} & \text{initial policy model } \pi_{\theta_{\text{init}}}\text{; reward models } r_\phi\text{; task prompts } \mathcal{D}\text{;}\ \text{hyperparameters } \epsilon, \beta, \mu \\ \hline 1 & \text{policy model } \pi_\theta \leftarrow \pi_{\theta_{init}} \\ 2 & \textbf{for } \text{iteration} = 1,\cdots,I \textbf{ do} \\ 3 & \qquad\text{reference model } \pi_{ref} \leftarrow \pi_{\theta} \\ 4 & \qquad\textbf{for } \text{step} = 1,\cdots,M \textbf{ do} \\ 5 & \qquad\qquad\text{Sample a batch } \mathcal{D}_b \text{ from } \mathcal{D} \\ 6 & \qquad\qquad\text{Update the old policy model } \pi_{\theta_{old}} \leftarrow \pi_{\theta} \\ 7 & \qquad\qquad\text{Sample } G \text{ outputs } \{o_i\}_{i=1}^G \sim \pi_{\theta_{old}} (\cdot \mid q) \text{ for each question } q \in \mathcal{D}_b \\ 8 & \qquad\qquad\text{Compute rewards } \{r_i\}_{i=1}^{G} \text{ for each sampled output } o_i \text{ by running } r_{\phi} \\ 9 & \qquad\qquad\text{Compute } \hat{A}_{i,t} \text{ for the } t\text{-th token of } o_i \text{ through group relative advantage estimation}\ \ \\ 10 & \qquad\qquad\textbf{for } \text{GRPO iteration} = 1,\cdots,\mu \textbf{ do} \\ 11 & \qquad\qquad\qquad\text{Update the policy model } \pi_{\theta} \text{ by maximizing the GRPO objective} \\ 12 & \qquad\qquad\textbf{end for} \\ 13 & \qquad\textbf{end for} \\ 14 & \qquad\text{Update } r_\phi \text{ through continuous training using a replay mechanism} \\ 15 & \textbf{end for} \\ \hline \textbf{Opt} & \pi_\theta \end{array} \end{array} } \]

Discussions

本文指出，代码训练从某种程度上加强了模型的数学推理能力. 本文还提出了下面的统一强化学习范式，并给出了一些实验结果.

\[\nabla_{\theta}\mathcal{J}_{\textcolor{red}{\mathcal{A}}}(\theta) = \mathbb{E}[\underbrace{(q,o) \sim \textcolor{red}{\mathcal{D}}}_{Data \ Source}]\left( \frac{1}{|o|} \sum_{t=1}^{|o|} \underbrace{GC_{{\mathcal{A}}}(q, o, t, \textcolor{red}{\pi_{{rf}}})}_{Gradient \ Coefficient} \nabla_{\theta}\log \pi_{\theta}(o_t | q, o_{<t})\right).\]

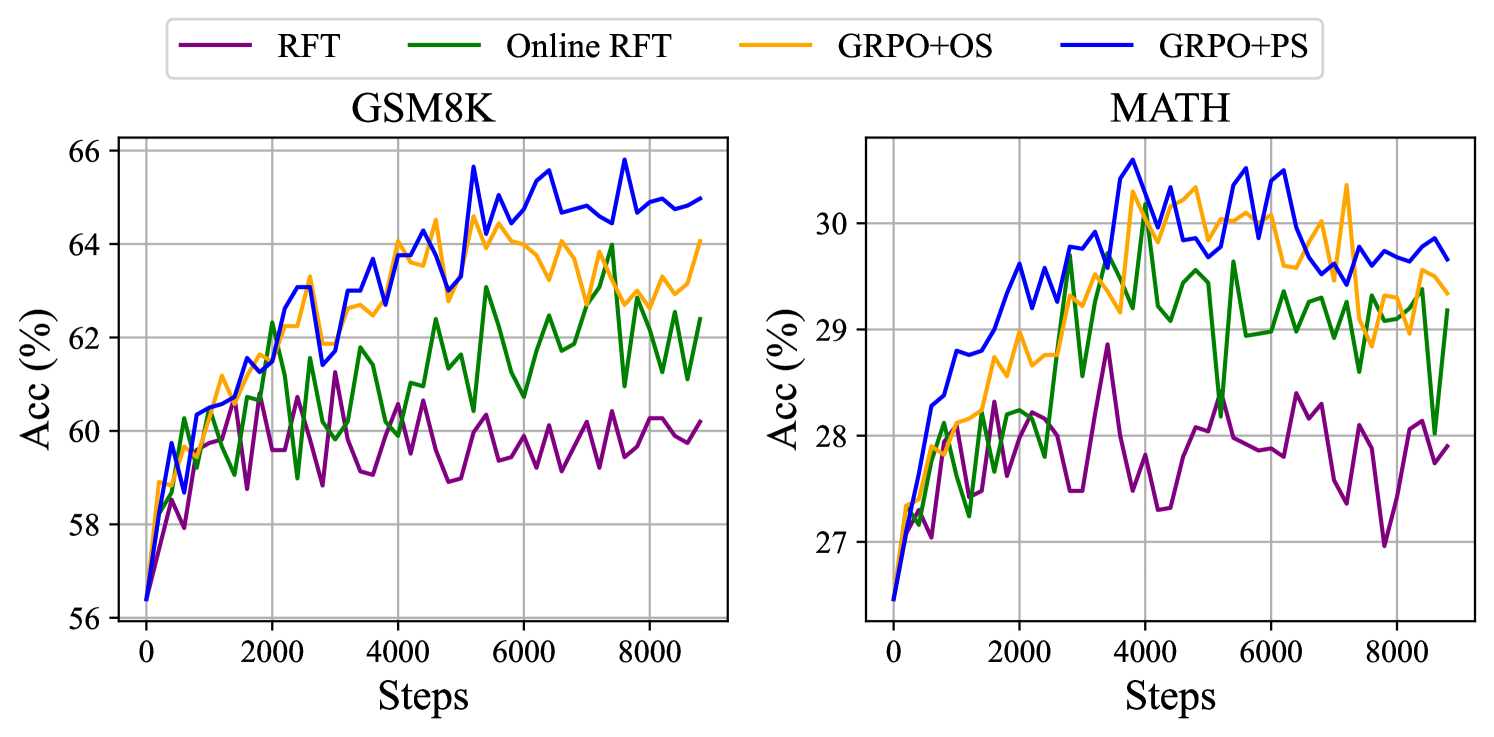
本文还提出了一些有关强化学习的有趣见解. 例如，RL 提升了 Maj@K 但对 Pass@K 没有影响，暗示 RL 通过使输出分布更加稳健来提高模型的整体性能. 同时，从三个方面来看：

Data Source. 在强化学习中，我们从 policy model 中抽样得到无标签问题和它们的答案. 改进的方向包括基于树搜索的采样策略，高效推理技术等，从而提高策略模型的探索效率.
Algorithms. 标注数据有时不可信，如何开发对噪声奖励信号具有鲁棒性的 RL 算法，如何使用 WEAK-STRONG 的对齐方式.
Reward Function. 如何增强奖励模型的泛化能力从而解决 out-of-distribution 的问题，如何反映奖励模型的不确定性，如何高效地构建高质量的 PRM 从而提供细粒度的训练信号.

同时，本文以一种统一的视角分析了 SFT, RFT, Online RFT, DPO, PPO, GRPO 算法. 具体来说：

Supervised Fine-tuning. 旨在最大化下面的目标.

\[\mathcal{J}_{SFT}(\theta)=\mathbb{E}_{q, o \sim P_{sft}(Q, O)}\left(\frac{1}{|o|}\sum_{t=1}^{|o|} \log \pi_\theta(o_t | q, o_{<t})\right).\]

数据源：用于 SFT 的数据集. 奖励函数：可以被视作人类选择. 梯度系数：恒为 \(1\).

Rejection Sampling Fine-tuning. 首先从 SFT 的 LLM 中采样多个输出，然后在具有正确答案的输出上训练 LLM. 旨在最大化下面的目标.

\[\mathcal{J}_{RFT}(\theta)= \mathbb{E}_{q \sim P_{sft}(Q), o \sim \pi_{sft}(O|q)}\left( \frac{1}{|o|}\sum_{t=1}^{|o|} \mathbb{I}(o) \log \pi_\theta(o_{t} | q, o_{<t})\right).\]

数据源：SFT 数据集中的问题与 SFT 模型的输出. 奖励函数：rule-based. 梯度系数：

\[GC_{RFT}(q, o, t) = \mathbb{I}(o)= \begin{cases} 1 & {\rm the \ answer \ of \ }o{\rm \ is \ correct} \\ 0 & {\rm the \ answer \ of \ }o{\rm \ is \ incorrect} \\ \end{cases}.\]

Online Rejection Sampling Fine-tuning. 从实时策略模型 \(\pi_\theta\) 中采样，而不是 SFT 模型.

\[\nabla_{\theta}\mathcal{J}_{OnRFT}(\theta)= \mathbb{E}_{q \sim P_{sft}(Q), o \sim \pi_{\theta}(O|q)}\left( \frac{1}{|o|}\sum_{t=1}^{|o|} {\mathbb{I}(o)} \nabla_{\theta}\log \pi_\theta(o_{t} | q, o_{<t})\right).\]

Direct Preference Optimization (DPO). 旨在最大化下面的目标.

\[\mathcal{J}_{DPO}(\theta) = \mathbb{E}_{q \sim P_{sft}(Q), o^+, o^- \sim \pi_{sft}(O|q)} \log \sigma \left( \beta \frac{1}{|o^+|}\sum_{t=1}^{|o^+|} \log \frac{\pi_{\theta}(o^+_t | q, o^+_{<t})}{\pi_{ref}(o^+_t | q, o^+_{<t})} - \beta \frac{1}{|o^-|}\sum_{t=1}^{|o^-|} \log \frac{\pi_{\theta}(o^-_{<t} | q, o^-_{<t})}{\pi_{ref}(o^-_{<t} | q,o^-_{<t})} \right) .\]

\[\begin{split} \nabla_{\theta}\mathcal{J}_{DPO}(\theta) = &\mathbb{E}_{q \sim P_{sft}(Q), o^+, o^- \sim \pi_{sft}(O|q)}\\ &\left( \frac{1}{|o^+|}\sum_{t=1}^{|o^+|} GC_{DPO} (q,o,t) \nabla_{\theta}\log\pi_{\theta}(o^+_t | q, o^+_{<t}) \right. - \left. \frac{1}{|o^-|}\sum_{t=1}^{|o^-|} GC_{DPO} (q,o,t) \nabla_{\theta}\log\pi_{\theta}(o^-_t | q, o^-_{<t}) \right). \end{split}\]

数据源：SFT 数据集中的问题与 SFT 模型的输出. 奖励函数：一般领域的人类偏好. 梯度系数：

\[ GC_{DPO}(q,o,t) = \sigma\left(\beta\log \frac{\pi_{\theta}(o^-_t | q, o^-_{<t})}{\pi_{ref}(o^-_t | q, o^-_{<t})} - \beta\log \frac{\pi_{\theta}(o^+_t | q, o^+_{<t})}{\pi_{ref}(o^+_t | q, o^+_{<t})}\right) . \]

Proximal Policy Optimization (PPO). 旨在最大化下面的目标

\[\mathcal{J}_{PPO}(\theta) = \mathbb{E}_{q \sim P_{sft}(Q), o \sim \pi_{\theta_{old}}(O|q)} \frac{1}{|o|} \sum_{t=1}^{|o|} \min \left[ \frac{\pi_\theta(o_{t} | q, o_{<t})}{\pi_{\theta_{old}}(o_{t} | q, o_{<t})} A_{t}, \text{clip} \left( \frac{\pi_\theta(o_{t} | q, o_{<t})}{\pi_{\theta_{old}}(o_{t} | q, o_{<t})}, 1 - \epsilon, 1 + \epsilon \right) A_{t} \right].\]

假如在每个探索阶段后只有一次更新，那么 \(\pi_{\theta_{old}}=\pi_{\theta}\). 于是

\[\mathcal{J}_{PPO}(\theta) = \mathbb{E}_{q \sim P_{sft}(Q), o \sim \pi_{\theta_{old}}(O|q)} \frac{1}{|o|} \sum_{t=1}^{|o|} \frac{\pi_\theta(o_{t} | q, o_{<t})}{\pi_{\theta_{old}}(o_{t} | q, o_{<t})} A_{t}.\]

\[\nabla_{\theta}\mathcal{J}_{PPO}(\theta) = \mathbb{E}{[q \sim P_{sft}(Q), o \sim \pi_{\theta_{old}}(O|q)]} \frac{1}{|o|} \sum_{t=1}^{|o|} A_t \nabla_{\theta}\log \pi_\theta(o_{t} | q, o_{<t}).\]

数据源：SFT 数据集中的问题与 policy model 的输出. 奖励函数：reward model. 梯度系数：\(GC_{PPO}(q, o, t, \pi_{\theta_{rm}}) = A_t.\)

其中 \(A_t\) 是优势，基于广义优势估计 GAE 得出，基于奖励 \(\{r_{\ge t}\}\) 和 value function \(V_{\psi}\) 得出.

Group Relative Policy Optimization (GRPO). 假设 \(\pi_{\theta_{old}}=\pi_{\theta}\).

\[ \begin{aligned}\mathcal{J}_{GRPO}(\theta) &= \mathbb{E}_{q \sim P_{sft}(Q), \{o_i\}_{i=1}^G \sim \pi_{\theta_{old}}(O|q)} \frac{1}{G}\sum_{i=1}^G\frac{1}{|o_i|} \\ & \left\{\sum_{t=1}^{|o_i|} \left[\frac{\pi_\theta(o_{i,t} | q, o_{i,<t})}{\pi_{\theta_{old}}(o_{i,t} | q, o_{i,<t})} \hat{A}_{i,t} - \beta (\frac{\pi_{ref}(o_{i,t}|q,o_{i,<t})}{\pi_{\theta}(o_{i,t}|q,o_{i,<t})}- \log\frac{\pi_{ref}(o_{i,t}|q,o_{i,<t})}{\pi_{\theta}(o_{i,t}|q,o_{i,<t})} - 1)\right]\right\}.\end{aligned} \]

\[\begin{split} \nabla_{\theta}\mathcal{J}_{GRPO}(\theta) & = \mathbb{E}_{q \sim P_{sft}(Q), \{o_i\}_{i=1}^G \sim \pi_{\theta_{old}}(O|q)}\frac{1}{G}\sum_{i=1}^G\frac{1}{|o_i|} \\ & \left\{\sum_{t=1}^{|o_i|} \left[\hat{A}_{i,t} + \beta \left(\frac{\pi_{ref}(o_{i,t}|o_{i,<t})}{\pi_{\theta}(o_{i,t}|o_{i,<t})} - 1\right)\right] \nabla_{\theta}\log \pi_\theta(o_{i,t} | q, o_{i,<t})\right\}. \end{split}\]

数据源：SFT 数据集中的问题与 policy model 的输出. 奖励函数：reward model. 梯度系数：

\[GC_{GRPO}(q, o, t, \pi_{\theta_{rm}}) = \hat{A}_{i,t} + \beta \left(\frac{\pi_{ref}(o_{i,t}|o_{i,<t})}{\pi_{\theta}(o_{i,t}|o_{i,<t})} - 1\right).\]

其中 \(\hat{A}_{i,t}\) 是基于分组的奖励分数计算的.

本页面最近更新：，更新历史
发现错误？想一起完善？在 GitHub 上编辑此页！
本页面贡献者：OI-wiki
本页面的全部内容在协议之条款下提供，附加条款亦可能应用